A következő eljárások alapja az alábbi publikáció volt:
Crofton, M.V.: On the theory of local probability applied to straight lines drawn at random in a plane
Philosophical Transactions of the Royal Society, 1868. 181-199.
A Crofton által leírt módszer kartometriai alkalmazása századunk ötvenes éveiben két lengyel matematikus, Steinhaus és Perkal nevéhez fűződik. Steinhaus a hossz paradoxonáról az alábbiakat írta [46]:
"A hossz paradoxona nem keverhető össze azzal a ténnyel, hogy minden fizikai mennyiség meghatározása (pl. terület, térfogat, tömeg, erő) hibákkal terhelt. Pl. a Visztula folyó bal partjának hosszát egyre növekvő pontossággal meghatározva a mért hossz tíz-, száz-, sőt ezerszerese is lehet annak, amit például egy iskolai atlasz segítségével meghatározhatunk. Ez az állítás nagyjából megfelel a valóságnak, mivel a természetben előforduló görbék többsége nem rektifikálható. De az állítás ellentétes azzal a hiedelemmel, hogy a nem rektifikálható görbék a matematikusok szüleményei és hogy a természetben található görbék visszafejthetők: éppen ez ellenkezője az igazság."
Ez a paradoxon vezette Steinhaust hosszmérési módszere, az ún. longiméter megalkotására. A módszer lényege egy olyan átlátszó fedvény alkalmazása, melyen egymástól d távolságra párhuzamos egyenesek találhatók (hasonlóan a Buffon-tűhöz). A mérendő vonalnak ni számú metszéspontja van a párhuzamosokkal. A fedvényt ![]() ˇk/m (ahol k = 1, 2, ..., m) szögekkel elforgatva, újabb nk értékeket nyerünk a fedvény k számú alkalmazásával. A mérést addig folytatjuk, amíg k eléri m értékét, ezt az értéket Steinhaus a mérés rendűségének nevezte. Eszerint egy m rendű vonal hossza:
ˇk/m (ahol k = 1, 2, ..., m) szögekkel elforgatva, újabb nk értékeket nyerünk a fedvény k számú alkalmazásával. A mérést addig folytatjuk, amíg k eléri m értékét, ezt az értéket Steinhaus a mérés rendűségének nevezte. Eszerint egy m rendű vonal hossza:
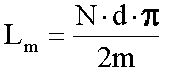 , ahol
, ahol 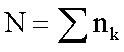
Steinhaus az m=6 és a d=2 mm értékeket ajánlotta, mint amelyek elégséges pontosságot adnak, de azt nem említette, hogy milyen célú mérésekhez [46].
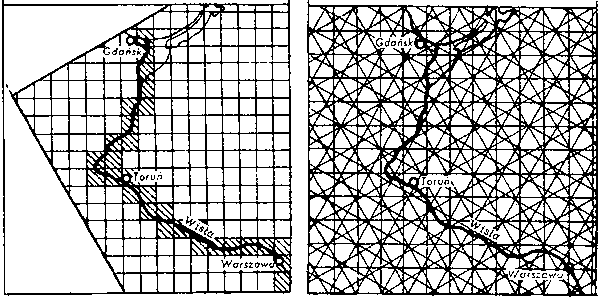
Maling [36] mérésekkel támasztotta alá Steinhaus kijelentését [46]. A táblázat Yorkshire partvonalának hosszát mutatja Steinhaus longiméterével mérve. Látható, hogy a mért hossz nő a rendűség növekedésével annak megfelelően, ahogy a mérés finomodásával is nő a mért hossz, de m=7 után a tendencia megváltozik, vagyis nincs értelme további méréseknek, mert ez nem növeli a pontosságot. (Az m=1, 2 esetnek nincs kartometriai jelentősége, hiszen valószínűségi módszerek alkalmazásakor a módszer ennél többszöri alkalmazása elengedhetetlen.) Steinhaus kutatásaiból nem derül ki, hogyan jutott ehhez az m=6 optimális értékhez: véletlenül, vagy mérésekkel alátámasztva.
| Rendűség | Átlagos hossz (km) | Szórás (km) |
|---|---|---|
| 1 | 176.54 | ±10.05 |
| 2 | 172.95 | ±9.79 |
| 3 | 173.31 | ±8.74 |
| 4 | 175.46 | ±6.61 |
| 5 | 178.26 | ±4.17 |
| 6 | 179.36 | ±3.22 |
| 7 | 178.85 | ±2.42 |
| 8 | 179.16 | ±3.00 |
| 9 | 178.44 | ±2.73 |
| 10 | 177.33 | ±3.40 |